色彩空间的作用及各空间之间的转换

QSTX2024/8/7大约 3 分钟

色彩空间的作用及各空间之间的转换

线性空间和Gamma空间

下面是Unity生成的线性空间和Gamma空间的颜色强度图像，可以看到线性空间下能表征暗部（视觉意义上的暗部）的数值区域十分有限，而Gamma空间下明暗很均匀。

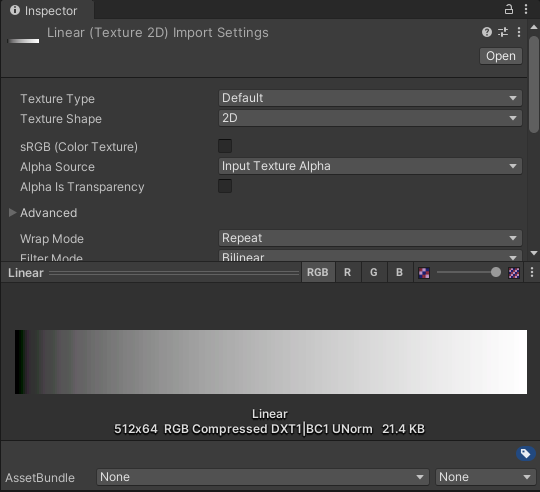
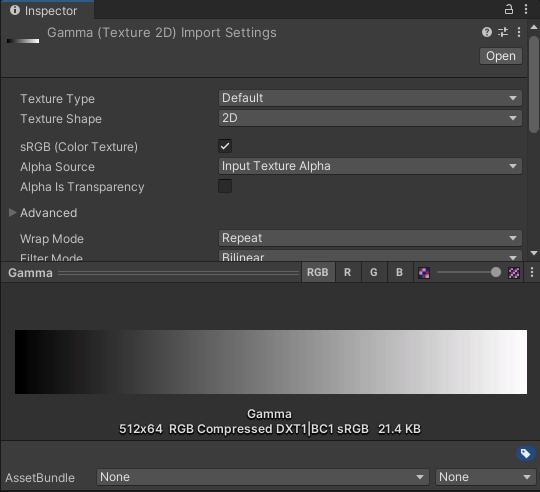
首先要明确两者所描述物理量的不同：

线性空间是色彩在物理强度上的线性表达
Gamma空间是色彩在人眼感知强度上的线性表达

因为人眼对光线的感知强度与光线的物理强度之间是非线性的，想要将感知强度真真正正地记录到数据中需要进行转换。

以物理强度为横轴、感知强度为纵轴，拟合得到一个幂函数曲线y=x^2.2 以感知强度为横轴、物理强度为纵轴，拟合得到一个幂函数曲线y=x^0.4545

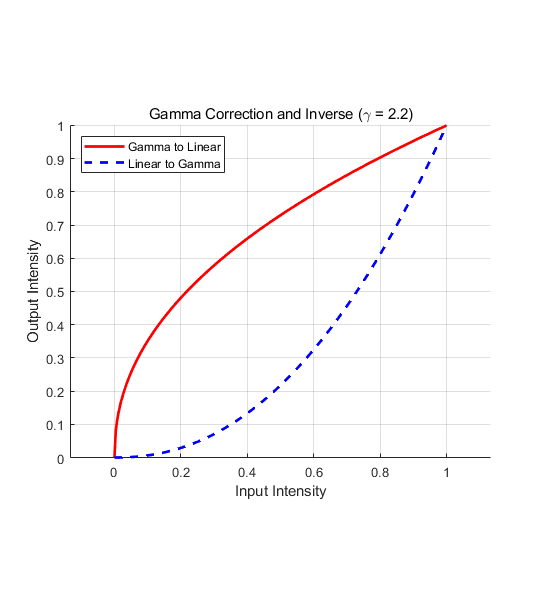
附件

1.Unity生成线性空间和Gamma空间图片的自定义窗口

using System.IO;
using UnityEditor;
using UnityEngine;

public class TextureCreator : EditorWindow
{
    [MenuItem("QSTX Tools/TextureCreator")]
    public static void OpenWindow()
    {
        GetWindow<TextureCreator>();
    }

    private const string filefolder = "LinearGamma/";
    private string filename = "";
    private bool is_gamma = false;
    private void OnGUI()
    {
        //filename = GUILayout.TextField(filename);
        is_gamma = GUILayout.Toggle(is_gamma, "is_gamma");
        if (GUILayout.Button("生成"))
        {
            filename = (is_gamma ? "Gamma" : "Linear");
            Create(filename,is_gamma);
        }
    }

    void SaveTextureAsPNG(Texture2D texture, string fileName)
    {
        // 将Texture转换为PNG格式
        byte[] bytes = texture.EncodeToPNG();

        // 将文件保存到项目文件夹下
        string filePath = Path.Combine(Application.dataPath, Path.Combine(filefolder,fileName));
        File.WriteAllBytes(filePath, bytes);
        Debug.Log("Texture saved to " + filePath);
    }

    void Create(string filename,bool is_gamma)
    {
        // 创建一个新的Texture2D对象
        int width = 512;
        int height = 64;
        Texture2D texture = new Texture2D(width, height,TextureFormat.RGBAFloat,0,!is_gamma);

        // 填充Texture，设置每个像素的颜色
        for (int y = 0; y < height; y++)
        {
            for (int x = 0; x < width; x++)
            {
                float stren = x / (float)width;
                Color strenColor = new Color(stren, stren, stren);
                texture.SetPixel(x, y, strenColor);
            }
        }

        // 应用设置的像素颜色
        texture.Apply();

        // 保存Texture为PNG文件
        SaveTextureAsPNG(texture, $"{filename}.png");
        AssetDatabase.Refresh();
    }
   Color GammaToLinearSpace (Color sRGB)
    {
        // Approximate version from http://chilliant.blogspot.com.au/2012/08/srgb-approximations-for-hlsl.html?m=1
        return sRGB * (sRGB * (sRGB * 0.305306011f + new Color(0.682171111f,0.682171111f,0.682171111f)) +  new Color(0.012522878f,0.012522878f,0.012522878f));

        // Precise version, useful for debugging.
        //return half3(GammaToLinearSpaceExact(sRGB.r), GammaToLinearSpaceExact(sRGB.g), GammaToLinearSpaceExact(sRGB.b));
    }
    float GammaToLinearSpaceExact (float value)
    {
        if (value <= 0.04045F)
            return value / 12.92F;
        else if (value < 1.0F)
            return Mathf.Pow((value + 0.055F)/1.055F, 2.4F);
        else
            return Mathf.Pow(value, 2.2F);
    }

    Vector4 Pow(Vector4 v, float p)
    {
        return new Vector4(Mathf.Pow(v.x, p), Mathf.Pow(v.y, p), Mathf.Pow(v.z, p), Mathf.Pow(v.w, p));
    }
    Color LinearToGammaSpace (Color linRGB)
    {
        Vector4 colorVector4 = linRGB;
        colorVector4 = Vector4.Max(colorVector4,Vector4.zero);
        // An almost-perfect approximation from http://chilliant.blogspot.com.au/2012/08/srgb-approximations-for-hlsl.html?m=1
        return Vector4.Max(1.055f * Pow(linRGB, 0.416666667f) - new Vector4(0.055f,0.055f,0.055f,0.055f), Vector4.zero);

        // Exact version, useful for debugging.
        //return half3(LinearToGammaSpaceExact(linRGB.r), LinearToGammaSpaceExact(linRGB.g), LinearToGammaSpaceExact(linRGB.b));
    }
    float LinearToGammaSpaceExact (float value)
    {
        if (value <= 0.0F)
            return 0.0F;
        else if (value <= 0.0031308F)
            return 12.92F * value;
        else if (value < 1.0F)
            return 1.055F * Mathf.Pow(value, 0.4166667F) - 0.055F;
        else
            return Mathf.Pow(value, 0.45454545F);
    }
}

2.Matlab绘制转换函数曲线

% 定义 Gamma 值
gamma_value = 2.2;

% 定义输入亮度值（0 到 1 之间）
x = linspace(0, 1, 256);

% 计算 Gamma 校正后的输出值（Gamma 空间 -> 线性空间）
y_gamma_to_linear = x .^ (1 / gamma_value);

% 计算从线性空间到 Gamma 空间的输出值
y_linear_to_gamma = x .^ gamma_value;

% 绘制曲线
figure; % 创建新图形窗口
hold on; % 保持当前图像，使得可以在同一图上绘制多条曲线

% 绘制 Gamma 到线性空间的转换曲线
plot(x, y_gamma_to_linear, 'r-', 'LineWidth', 2, 'DisplayName', 'Gamma to Linear'); 

% 绘制线性空间到 Gamma 空间的转换曲线
plot(x, y_linear_to_gamma, 'b--', 'LineWidth', 2, 'DisplayName', 'Linear to Gamma');

% 设置图例位置为左上角
legend('Location', 'northwest');

% 设置 x 轴和 y 轴等长
axis equal;

% 设置图像属性
grid on; % 打开网格
xlabel('Input Intensity'); % x 轴标签
ylabel('Output Intensity'); % y 轴标签
title(['Gamma Correction and Inverse (\gamma = ', num2str(gamma_value), ')']); % 标题，显示 Gamma 值

hold off; % 释放图像